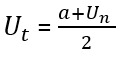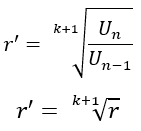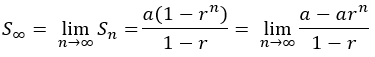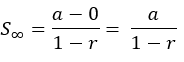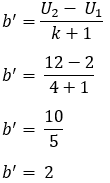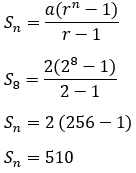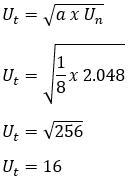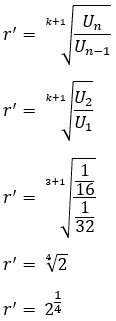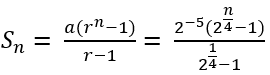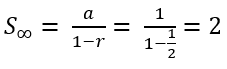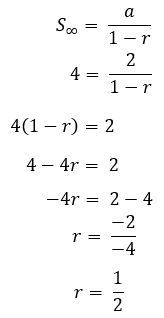Rumus Aritmatika Dan Geometri Beserta Contoh Soal Dan Pembahasannya

Artikel kali ini akan membahas mengenai rumus aritmatika dan geometri beserta contoh soal dan pembahasannya.

Aritmatika dan geometri merupakan topik yang kita pelajari di bangku sekolah dalam mata pelajaran matematika. Dimana ketika ujian nasional, ujian masuk perguruan tinggi ataupun ujian dalam melamar pekerjaan sering terdapat soal mengenai keduanya.

Tidak hanya itu, kita juga harus dapat membedakan antara barisan dan deret aritmatika ataupun barisan dan deret geometri, karena kaidah barisan dan deret dapat memudahkan kita dalam penyelesaian perhitungan, seperti bunga bank, kenaikan produksi, dan laba/rugi suatu usaha. Baiklah, mari kita simak penjabaran berikut ini!

Rumus Aritmatika

• Barisan Aritmatika

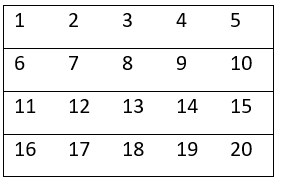
Coba perhatikan tabel diatas, amati berapa selisih bilangan dari kiri kita ke kanan kita? Dan kemudian, amati berapa selisih bilangan dari atas ke bawah ?

Dari hasil pengamatan, kita mendapati bahwa selisihnya dari satu barisan selalu tetap. Misalkan dari barisan kanan kita ke kiri kita : 1, 2, 3, 4, 5 (selisihnya 1).

5 – 1 = 4; 4 – 1 = 3; 3 – 1 = 2; 2 – 1 = 1

Dan dari barisan atas ke bawah : 1, 6, 11, 16 (selisihnya 5).

16 – 5 = 11; 11 – 5 = 6; 6 – 5 = 1

Barisan seperti ini disebut barisan aritmatika.

Selisih yang memiliki nilai tetap disebut beda dan dilambangkan dengan b. Secara umum dapat dikatakan bahwa jika U_n adalah rumus suku ke-n suatu barisan aritmatika, maka berlaku

b = U_n – U_n-1

Jika suku pertama (U₁) dilambangkan dengan a  dan beda dilambangkan dengan b, maka rumus suku ke-n barisan itu dapat diturunkan sebagai berikut.

U₁= a

U₂= U₁ + b                       = a + b

U₃= U₂ + b = (a + b) + b = a + 2b

U₄= U₃ + b = (a + 2b) + b = a + 3b

U₅= U₄ + b = (a + 3b) + b = a + 4b

Jadi, dapat dirumuskan suku ke-n dari barisan aritmatika adalah

U_n= a + (n – 1)b

Keterangan :

U_n= suku ke-n

a =  suku pertama

b = beda

n = banyak suku

• Deret Aritmatika

Jika suku-suku barisan aritmatika dijumlahkan akan diperoleh deret aritmatika. Misalkan U₁, U₂, U₃,…….,U_n merupakan suku-suku dari barisan aritmatika, maka U₁ + U₂ + U₃ +….+U_n disebut deret aritmatika. Deret aritmatika dari n ditulis dengan notasi S_n dengan U_n= a + (n – 1)b.

Jadi, rumus umum untuk deret aritmatika adalah

S_n= 1/2 n(a + U_n)

S_n= 1/2 n(2a + (n – 1)b)

Keterangan :

S_n= jumlah n suku deret aritmatika

a =  suku pertama

b = beda

U_n= suku ke-n

n = banyak suku

Menentukan suku ke-n barisan aritmatika jika diketahui rumus jumlah n suku pertamanya. Suku ke-n dapat ditentukan dengan rumus sebagai berikut.

U_n = S_n – S_n-1

• Suku Tengah Barisan atau Deret Aritmatika

Apabila diketahui barisan aritmatika berikut : U₁, U₂, U₃,…….,U_n, dengan banyaknya suku barisan aritmatika yang merupakan ganjil, maka terdapat sebuah suku tepat ditengah barisan tersebut yang membagi barisan menjadi 2 bagian yang sama. Misalkan suku tengah dari barisan tersebut adalah U_t. Maka untuk mencari suku tengah adalah sebagai berikut.

Keterangan :

U_t= suku tengah barisan aritmatika

a =  suku pertama

U_n= suku terakhir barisan aritmatika dengan banyaknya n ganjil

• Sisipan pada Barisan Aritmatika

Misalkan U₁, U₂, U₃,…….,U_n, adalah barisan aritmatika dengan suku awal U_1. Jika antara dua suku berurutan disisipkan k bilangan sedemikian rupa sehingga terbentuk barisan aritmatika baru, maka beda barisan aritmatika baru yang terbentuk adalah sebagai berikut.

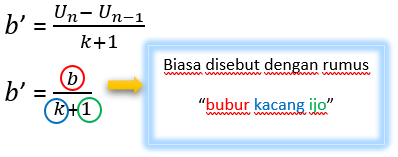
Keterangan :

b’= beda baru setelah sisipan

b = beda sebelum sisipan

k = bilangan yang disisipkan

Rumus Geometri

• Barisan Geometri

Coba kalian amati barisan 1, 2, 4, 8, 16,….Terlihat bahwa suku berikutnya diperoleh dengan mengalikan 2 pada suku sebelumnya. Barisan ini termasuk barisan geometri.

Jadi, dapat disimpulkan secara umum, barisan geometri  adalah suatu barisan bilangan yang setiap sukunya diperoleh dari suku sebelumnya dikalikan dengan suatu bilangan tetap (konstan). Bilangan yang tetap tersebut dinamakan rasio (pembanding) dan disimbolkan dengan r.

Jika U₁, U₂, U₃,U₄…….,U_n barisan geometri dengan U_n  adalah rumus ke-n, dan rasio r, berlaku :

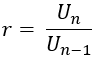
Rumus umum suku ke-n barisan geometri dengan suku pertama (U₁) dinyatakan a dan rasio r, dapat diturunkan sebagai berikut.

U₁= a

U₂= U₁ x r = ar

U₃= U₂ x r = ar²

U₄= U₃ x r = ar³

:        :

U_n= U_n-1 x r = ar^n-2 x r = ar^n-1

Dengan demikian diperoleh barisan geometri a, ar, ar², …., ar^n-1.

Jadi, rumus umum suku ke-n barisan geometri adalah

U_n= ar^n-1

Keterangan :

U_n = suku ke-n

a = suku pertama

r = rasio

n = banyak suku

• Deret Geometri

Jika U₁, U₂, U₃,U₄…….,U_n merupakan barisan geometri maka U_{1 +} U_{2 +} U_{3 +} U₄ +…..+ U_n  adalah deret geometri dengan U_n = ar^n-1.

Rumus umum untuk menentukan jumlah n suku pertama dari deret geometri dapat diturunkan sebagai berikut.

Misalkan S_n  notasi dari jumlah n suku pertama.

S_n = U_{1 +} U_{2 +} U₃ +…..+ U_n

S_n = a ₊ ar ₊ ar² +…..+ ar^n-1…………………………………………………………………(1)

Jika kedua ruas dikalikan r, maka

rS_n = ar ₊ ar²  ₊ ar³ +…..+ arⁿ………………………………………………………………(2)

Dari selisih persamaan (1) dan (2), dapat kita peroleh

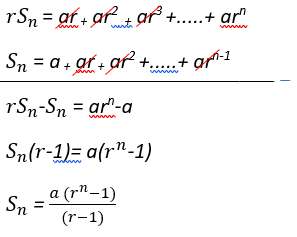
Jadi, rumus jumlah n suku pertama dari deret geometri, yaitu sebagai berikut.

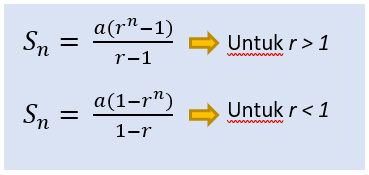
Keterangan :

S_n = jumlah n suku pertama

a = suku pertama

r = rasio

n = banyak suku

• Suku Tengah Barisan atau Deret Geometri

Misal diketahui barisan geometri berikut : U₁, U₂, U₃,U₄…….,U_n (banyaknya suku adalah ganjil). Suku tengah dari barisan tersebut adalah U_t, maka rumusnya yaitu sebagai berikut.

Keterangan :

U_t= suku tengah barisan geometri

a =  suku pertama

U_n= suku terakhir barisan geometri dengan banyaknya n ganjil

• Sisipan pada Barisan Geometri

Apabila dalam barisan geometri disisipkan k bilangan sedemikian rupa diantara dua suku berurutan, sehingga terbentuk barisan geometri baru. Maka dalam mencari rasio barunya dapat dirumuskan sebagai berikut.

Keterangan :

r’= rasio baru setelah sisipan

r = rasio sebelum sisipan

k = bilangan yang disisipkan

• Deret Geometri Tak Berhingga

Deret geometri tak berhingga merupakan deret geometri yang tidak dapat dicacah banyak seluruh sukunya. Perhatikan contoh berikut ini!

a. 1 + 2 + 4 + 8+….

b. 5 – 10 + 20 – 40 +…..

c. 1 + 1/2 + 1/4 + 1/8 +….

d. 9 – 3 + 1 – 1/3 +…..

Deret-deret di atas merupakan contoh deret geometri tak berhingga. Perhatikan contoh a dan b. Deret tersebut merupakan deret divergen, yaitu deret yang tidak menuju ke suatu nilai tertentu dan memiliki rasio r dengan | r | > 1.

Selanjutnya, contoh c dan d merupakan deret konvergen, yaitu deret yang menuju ke suatu nilai tertentu dan memiliki rasio r dengan | r | < 1.

Pada deret konvergen, jumlah suku-sukunya tidak akan melebihi suatu harga tertentu, tetapi akan mendekati harga tertentu. Harga tertentu ini disebut jumlah tak berhingga suku yang dinotasikan dengan S_∞. Nilai S_∞  merupakan nilai pendekatan (limit) seluruh suku (S_n) dengan n  mendekati tak berhingga. Oleh karena itu, rumus deret tak berhingga dapat diturunkan dari deret geometri dengan suku pertama a, dan n→∞.

Karena deret konvergen (| r | < 1 ), untuk n→∞, maka arⁿ→ 0 sehingga

Jadi, rumus jumlah deret geometri tak berhingga adalah

Itulah penjabaran mengenai rumus aritmatika dan geometri beserta contoh soal dan pembahasannya. Semoga bermanfaat !

Editor: Muchammad Zakaria

Afni Mediarti

Seseorang yang berusaha menjadi sahabat ‘waktu’