Rumus Bangun Ruang Beserta Contoh soal dan Pembahasannya

Kamu pasti sudah sering mendengar kata bangun ruang saat belajar matematika di sekolah. Jenis jenis dari bangun ruang bermacam-macam. Bangun ruang dapat diartikan seperti suatu benda atau ruangan dengan bentuk tiga dimensi yang memiliki isi dan juga volume, dan mempunyai batas (sisi-sisi).

Nah, bangun runag tersebut contohnya ialah kubus, balok, prisma segitiga, limas segiempat, limas segitiga, kerucut, tabung, dan bola.

Masing-masing bangun ruang tersebut mempunyai luas permukaan maupun bolumenya. Untuk lebih memahami mengenai rumus yang dipakai untuk mencarinya, yuk disimak penjelasan mengenai rumus bangun ruang dan contoh soalnya dibawah ini:

[ez-toc]

Rumus Bangun Ruang

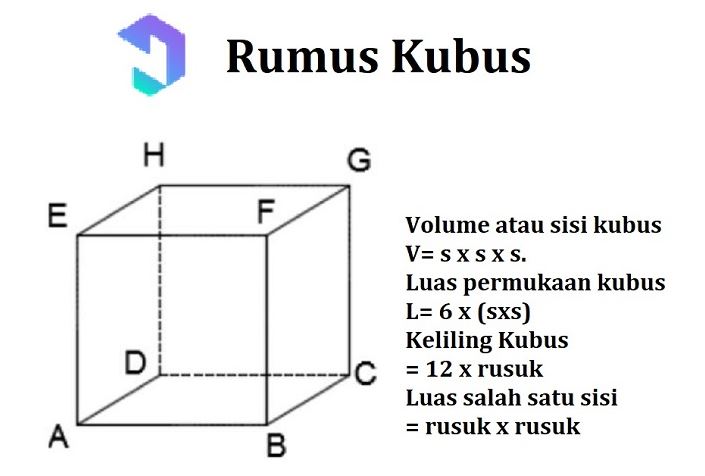
1. Kubus

Kubus itu apa sih? Kubus adalah bangun ruang yang sisinya datar, dimana semua rusuknya sama panjang serta semua sisi bentuk persegi. Contohnya dadu, rubik, kardus, dan lain-lain.

Sebelum membahas rumus bangun runagnya ketahui dulu ya, sifat dari kubus itu apa sih? Nah, ini dia sifat dari kubus itu:

Sift-sifat dari kubus:

• Semua sisi kubus berbentuk persegi panjang
• Memiliki 8 buah titik sudut
• Memiliki 12 buah rusuk sama panjang
• Memiliki 12 buah diagonal bidang (diagonal sisi) sama panjang
• Memiliki 4 buah diagonal yang sama panjang
• Memiliki 6 buah bidang sisi
• Memiliki 6 buah bidang diagonal berbentuk persegi panjang

Karena kubus merupakan bangun ruang tentu ada hal yang perlu kita hitung dong, seperti volumenya atau luas permukaannya. Ini adalah beberapa rumus yang bisa kamu pakai untuk menyelesaikan permasalahan dalam kubus:

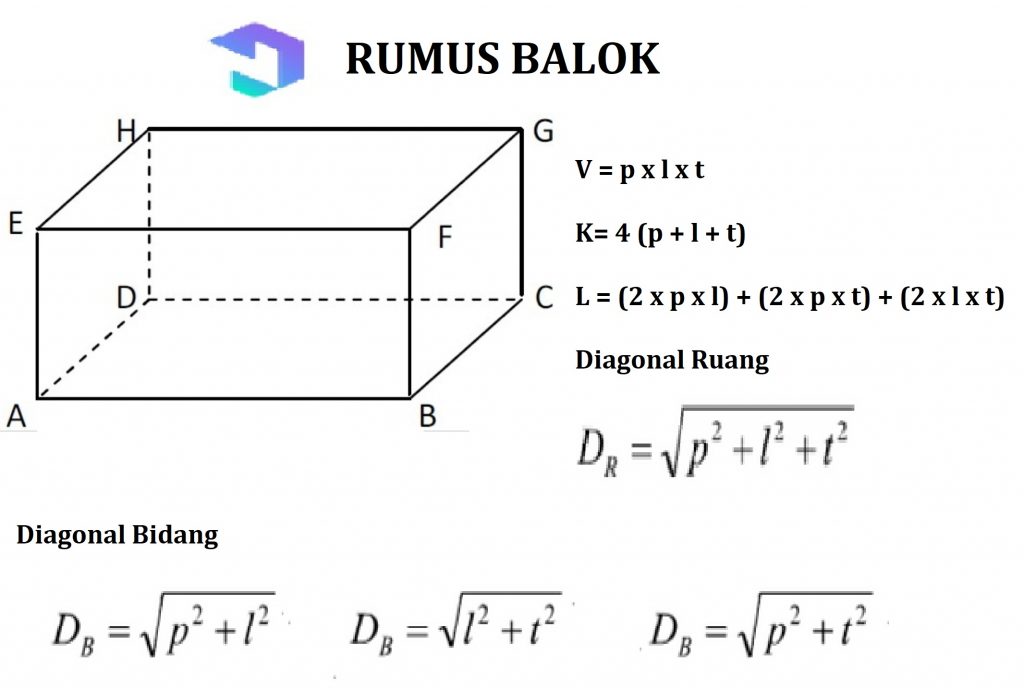
2. Balok

Bangun ruang sisi datar yang kedua ialah balok, dengan 3 pasang sisi dengan ukuran dan bentuk serta saling berhadapan. Bentuk sisinya persegi panjang.

Sifat-sifat dari balok:

• Memiliki sisi dengan bentuk persengi panjang
• Memiliki rusuk-rusuk sejajar dengan ukuran yang sama panjang
• Memiliki diagonal bidang yang berhadapan dan sama panjang
• Memiliki diagonal ruang yang sama panjang

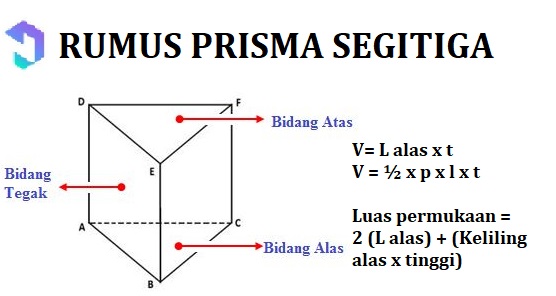
3. Prisma Segitiga

Prisma ialah bangun ruang yang memiliki bidang alas dan bidang atas yang kongruen dan sejajar. Alasan kenapa kongruen dan sesejar, ya karena sisi lain yang dimiliki prisma ialah tegak, dan bentuknya jajargenjang atau persegi panjang. Kongruen ialah sebangun dan sama.

Ada beberapa jenis prisma seperti prisma segilima, prisma segiempat, dan prisma segitiga. Yang membedakannya ialah jumlah dari bentuk alas dan atap yang dimilikinya.

Sifat-sifat dari prisma segitiga:

• Memiliki atap dan alas yang kongruen sebanyak 3 buah.
• Setiap sisi sampingnya seperti jajargenjang dan persegi panjang
• Umumnya memiliki rusuk yang tegak (bebrapa ada yang tidak tegak)
• Setiap diagonal bidang pada sisi yang sama, memiliki ukuran yang sama

Berikut ini rumus yang umum digunakan dalam mencari luas permukaan, volume prisma segitiga:

4. Limas Segiempat

Limas segiempat merupakan bangun ruang yang memiliki alas berbentuk segiempat. Biasanya limas memiliki bidang sisi yang tegak dan berbentuk segitiga, dan bertumpu pada satu titik karena berpotongan.

Berikut ini adalah rumus-rumus yang bisa digunakan dalam limas segiempat:

5. Limas Segitiga

Limas segitiga merupakan bangun ruang yang memiliki alas berbentuk segitiga. Biasanya limas memiliki bidang sisi yang tegak dan berbentuk segitiga, dan bertumpu pada satu titik karena berpotongan. Yang membedakan nama limas ialah bentuk alas yang dilikinya, seperti limas  segilima, limas segiempat, serta limas segitiga.

Berikut ini adalah rumus-rumus yang bisa digunakan dalam limas segitiga:

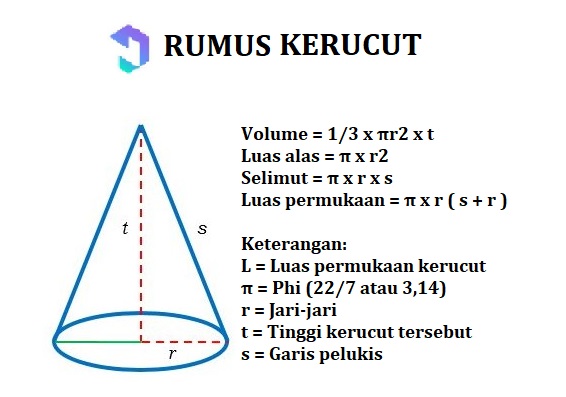
6. Kerucut

Kerucut merupakan bangun ruang dengan alas yang berbentuk lingkaran serta memiliki bidang sisi selimut dan terbentuk dari lingkaran seperti irisan. Kamu pasti sering melihat topi ulang tahun atau topi caping untuk petani. Nah, itu adalah contoh bentuk kerucut.

Ciri ciri dari kerucut:

• Memiliki 2 buah rusuk
• Memiliki titik sudut satu sebagai pertemuan dari titik sudutnya
• Memiliki 2 buah bidang sisi (bidang sisi dar lingkaran terdiri dari satu dan sebagai alas serta bidang selimut satu)

Beikut ini adalah rumus-rumus yang dapat digunakan dalam menyelesaikan soal-soal dalam bangun ruang kerucut:

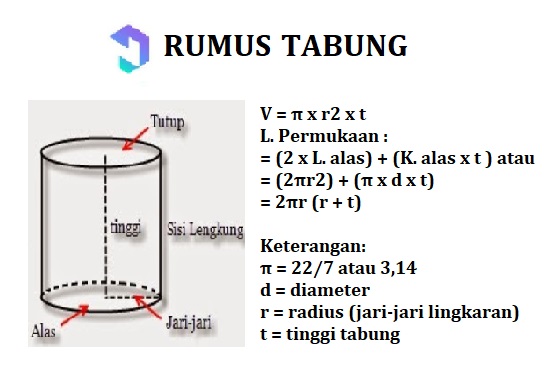
7. Tabung

Tabung merupakan bangun ruang yang terdiri dari alas dan tutup yang bentuknya lingkaran, serta memiliki selimut yang melengkung, dari sisi persegi panjang.

Sifat-sifat dari tabung:

• Memiliki alas dan tutup berukuran sama
• Memiliki 2 rusuk
• Memiliki 3 bidang (2 lingkaran dan 1 persegi panjang)
• Tidak memiliki titik sudut

Rumus umum untuk menghitung luas dan volume tabung:

8. Bola

Kita sangat sering melihat bola di kehidupan sehari-hari, bahkan sebagian dari kamu sangat menyenangi permainan bola. Yap, bola merupakan salah satu bangun ruang yang mempunya luas permukaan dan juga volume. Hal ini juga berhubungan kenapa bola bisa di giring dan dikendalikan dengan mudah karena kedua hal tersebut jawabannya.

Sifat-sifat bola:

• Tidak memiliki titik sudut dan rusuk
• Mempunyai jarak yang sama ke titik pusat pada titik bidang lengkungnya.

Berikut ini adalah rumus untuk mencari volume dan luas permukaan bola:

Contoh Soal+Pembahasannya

1. Sebuah rubik mempunyai panjang sisi 5 cm. Berapakah volume rubik tersebut?

Jawab:

V = s x s x s

= 5 x 5 x 5

= 125

Jadi volume rubik tersebut 125 cm³

2. Sebuah balok mempunyai panjang 8 cm, lebar 5 cm dan tinggi 4 cm. Berapakah keliling dari balok tersebut?

K = 4 (p x l x t)

= 4 (8 x 5 x 4)

= 640

Jadi keliling balok tersebut ialah 640 cm

3. Carilah berapa volume prisma segitiga jika luas alasnya 16 cm dan tingginya 10 cm !

Jawab:

V = L alas x t

= 16 x 10

= 160

Jadi volumenya 160 cm²

4. Hitunglah berapa volume dari limas segiempat jika panjangnya 6 cm, lebar 4 cm dan tinggi 9 cm

Jawab:

V = 1/3 (p x l x t)

= 1/3 (6 x 4 x 9)

= 71

Jadi volume limas segiempat adalah 72 cm²

5. Hitunglah berapa volume limas segitiga jika luas alasnya 24 cm dan tingginya 5 cm?

Jawab:

V = 1/3 (L alas x t)

= 1/3 (24 x 5)

= 40

Jadi luas permukaannya ialah 40 cm²

6. Sebuah topi ulang tahun mempunyai jari-jari 7 cm berapakah luas alas topi tersebu?

Jawab: 

L alas = πr²

= 22/7 x 7²

= 154

Jadi luas alas topi ulang tahun ialah 154 cm

7. Jari-jari sebuah tabung 15 cm. Jika tingginya 20 cm, maka volume tabung tersebut adalah….

Jawab:

V =πr²t

= 3,14 x 15² x 20

= 14.130

Jadi volume tabung ialah 14.130 cm²

8. Roda sepeda mempunyai jari-jari 14 cm. Tentukanlah luas permukaan roda sepeda tersebut!

Jawab:

L = 4πr²

= 4 x 22/7 x 14²

= 2464

Jadi luas permukaan roda sepeda yang jari-jarinya 14 cm adalah 2464 cm²

Itulah pembahasan tentang rumus bangun ruang (luas permukaan dan volume masing-masing bangun ruang) lengkap disertai contoh soal dan pembahasannya. Semoga bermanfaat dan mudah dipahami!

Editor: Muchammad Zakaria