Kegiatan berhitung pasti sudah Anda lakukan sejak dulu ketika masih balita hingga sekarang. Karena hitung menghitung angka selalu terjadi pada kehidupan setiap orang maka tidak heran apabila matematika menjadi mata pelajaran yang sudah diajarkan bahkan sejak taman kanak-kanak.
Tentunya level kesulitan pelajaran matematika di setiap jenjang pendidikan berbeda. Uniknya, pelajaran matematika selalu menjadi mata pelajaran yang akan menentukan daya kepintaran seseorang.
Semakin bagus nilai matematika Anda maka Anda akan semakin di anggap sebagai orang yang pintar. Mungkin hal ini juga didasari pada fakta jika beberapa soal matematika ada yang sangat sulit dikerjakan. Sehingga ahli matematika sering dianggap sebagai orang jenius.
Rumus Trapesium
Pengertian dari trapesium adalah sebuah bangun datar yang mempunyai dua dimensi dan disusun oleh 4 buah sisi yang sejajar namun tidak sama panjang. Trapesium juga terbentuk dari 4 buah rusuk dimana yang 2 rusuknya juga saling sejajar tetapi memiliki panjang yang berbeda. Bangun trapesium memiliki beberapa sifat yang membedakannya dengan bangun yang lain, diantaranya adalah:
- Memiliki 1 simetri putar
- Memiliki titik sudut yang tumpul minimal 1 sudut
- Memiliki 4 buah titik sudut
- Memiliki 2 sisi sejajar dengan panjang yang berbeda
- Trapesium merupakan bangun datar dengan 4 buah sisi atau quadrilateral
Berbicara mengenai trapesium, tentunya Anda sudah tahu jika untuk menghitung luas dan keliling trapesium dibutuhkan sebuah rumus. Adapun rumus dari luas dan keliling trapesium adalah sebagai berikut ini:
A. Rumus Luas Trapesium
Rumus luas trapesium pada umumnya adalah:
Luas = ½ × jumlah rusuk sejajar × tinggi
Namun, rumus diatas bisa berubah dan disesuaikan dengan bentuk trapesium. Ada 3 bentuk trapesium, yaitu trapesium siku-siku, trapesium sama kaki, dan trapesium sembarang. Penjelasan rumus untuk menghitung luas pada ketiga jenis trapesium ini adalah:
1. Rumus Luas Trapesium Siku-Siku
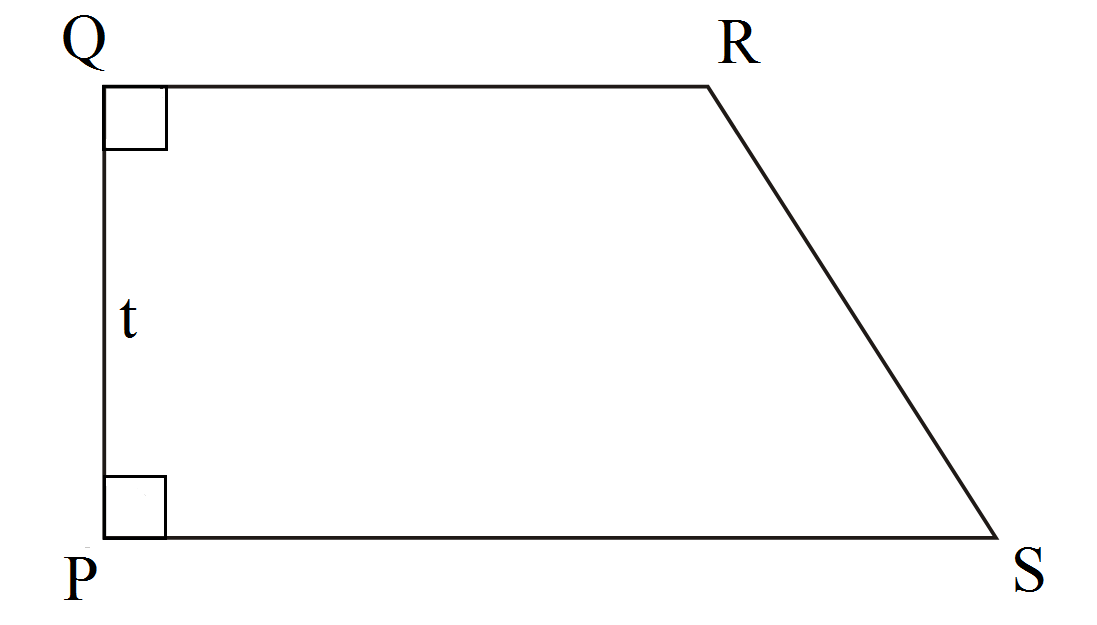Seperti namanya, trapesium siku-siku merupakan sebuah bangun trapesium dengan dua sudut siku-siku atau sisi yang sejajar dan saling tegak lurus dengan tinggi trapesium. Atau bisa dibilang salah satu sudut di trapesium siku-siku mempunyai besar 90°.
Rumus luas trapesium siku-siku PQRS : ( PQ + RS ) × t / 2
2. Rumus Luas Trapesium Sama Kaki
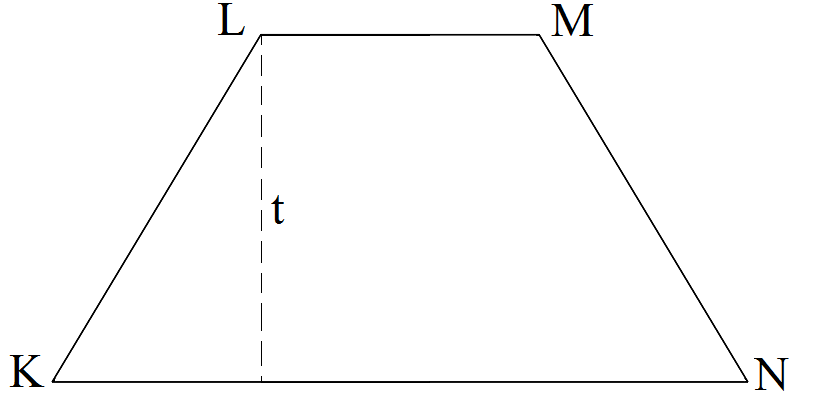Selain trapesium siku-siku, jenis bangun trapesium yang lainnya ada trapesium sama kaki. Dimana trapesium sama kaki adalah trapesium yang memiliki satu sisi simetri lipat dan rusuk yang sama panjang serta sejajar. Untuk lebih lengkapnya bisa Anda lihat dari gambar diatas.
Rumus luas trapesium sama kaki KLMN : ( LM + KN ) × t / 2
3. Rumus Luas Trapesium Sembarang
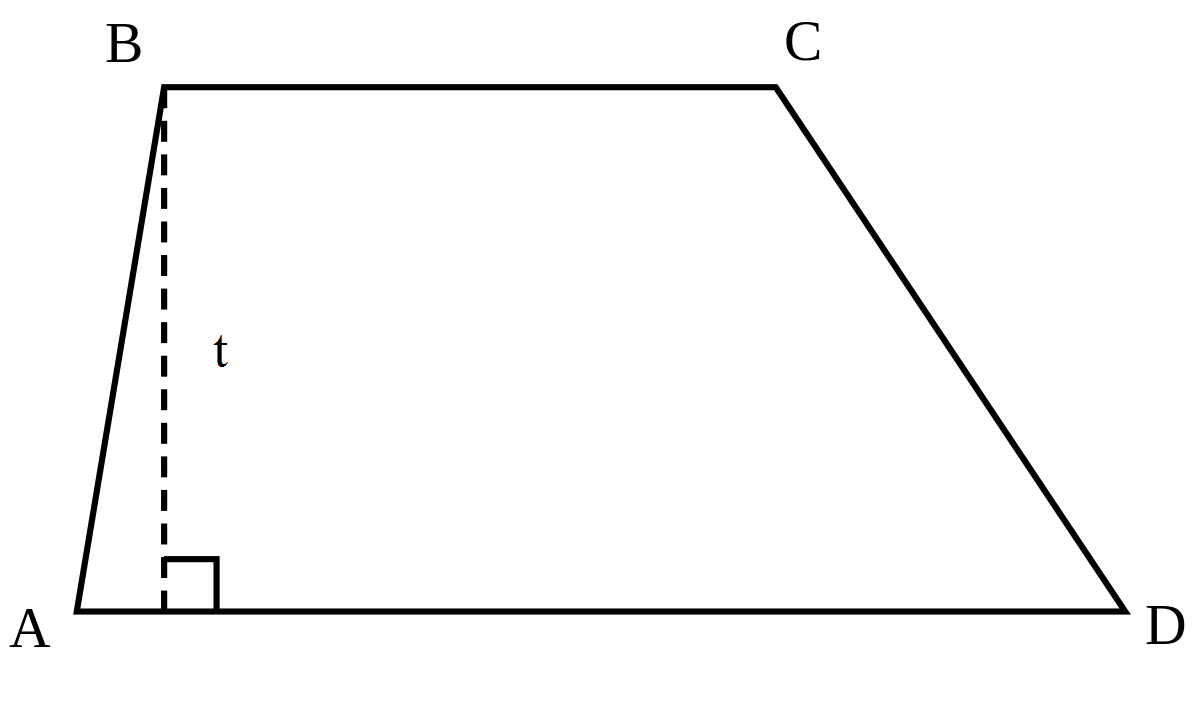Dari gambar diatas tentunya Anda sudah tahu mengapa trapesium ini disebut sebagai trapesium sembarang. Ini karena pada trapesium sembarang ABCD diatas, tidak ada simetri lipat sama sekali. Bahkan ukuran rusuknya juga tidak sama panjang serta tidak beraturan.
Rumus trapesium sembarang ABCD : ( BC + AD ) × t / 2
B. Rumus Keliling Trapesium
Untuk mengetahui keliling sebuah trapesium maka Anda harus memakai rumus keliling trapesium terlebih dahulu. Sebab rumus luas trapesium hanya dapat dipakai untuk menentukan luas saja, dan rumus keliling trapesium dipakai untuk menentukan keliling dari setiap jenis trapesium.
Rumus keliling trapesium : AB + BC + CD + DA
Dari rumus diatas dapat diambil kesimpulan jika keliling trapesium didapat dari penjumlahan semua sisi yang dimiliki oleh sebuah bangun trapesium.
1. Rumus Keliling Trapesium Siku-Siku
Pada trapesium siku-siku juga terdapat rumus kelilingnya, yaitu:
Keliling Trapesium Siku-siku PQRS = PQ + QR + RS + SP
2. Rumus Keliling Trapesium Sama Kaki
Sedangkan rumus keliling trapesium sama kaki adalah:
Keliling Trapesium Sama Kaki KLMN = KL + LM + MN + NK
3. Rumus Keliling Trapesium Sembarang
Pada dasarnya, rumus keliling trapesium dengan berbagai tipe sama saja. Rumus keliling untuk trapesium sembarang ialah:
Keliling Trapesium Sembarang ABCD = AB + BC + CD + DA
Dari rumus ketiga rumus keliling berbeda jenis pada bangun trapesium diatas dapat di simpulkan, apapun bentuk trapesiumnya maka rumus kelilingnya tetap satu. Namun pada trapesium tidak hanya terdapat rumus luas dan keliling yang biasa saja akan tetapi ada rumus yang memakai teorema pythagoras utamanya bagi trapesium siku-siku. Rumusnya adalah:
Rumus tinggi trapesium siku-sikuÂ
Rumus sisi miring (c) trapesium siku-siku
Rumus sisi alas (a) trapesium siku-siku
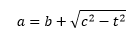
Contoh Soal Trapesium dan Pembahasan
Setelah mempelajari mengenai apa itu trapesium, sifat-sifat yang dimiliki oleh trapesium dan rumus yang dimiliki oleh trapesium. Maka tidak lengkap rasanya jika tidak mencoba untuk mengerjakan beberapa soal mengenai trapesium. Beberapa contoh soal trapesium dan penyelesaiannya dibawah ini bisa Anda jadikan materi untuk belajar.
1. Sebuah trapesium memiliki sisi sejajar 8 cm dan 22 cm serta tinggi 6 cm. Berapakah luas trapesium tersebut?
Jawab:
Luas trapesium = jumlah sisi sejajar x tinggi / 2 = ( 8 + 22 ) × 6 / 2 = 30 × 3 = 90 cm2
2. Jika panjang kedua sisi miring pada trapesium pada soal 1 adalah 5, berapakah keliling trapesium?
Jawab:
Keliling trapesium = panjang semua rusuk = 8 + 22 + 5 + 5 = 40 cm.
3. Pehatikan gambar dibawah ini!
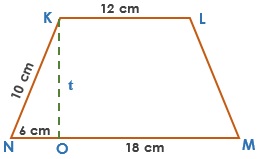Hitunglah luas dan keliling trapesium sama kaki diatas!
Jawab:
Karena trapesium KLMN diatas merupakan trapesium sama kaki maka panjang LM = KN = 10 cm.
Sehingga kelilingnya:
Keliling = KL + LM +MN + KN
Keliling = 12 + 10 + (18 + 6) + 10 = 56 cm
Luas trapesium:
Untuk menghitung luasnya, terlebih dahulu kita harus mengetahui tinggi trapesium tersebut (panjang sudut K dan O). Perhatikan pada gambar, sudut N K O membentuk sebuah segitiga siku-siku sehingga untuk mencari panjang sudut K dan O digunakan rumus Phytagoras berikut:
K O = tinggi trapesium = 8 cm.
Sehingga:
- Luas = ½ × jumlah sisi sejajar × tinggi
- Luas = ½ × (KL + MN) × KO
- Luas = ½ × (12 + 24) × 8 = 144 cm².
4. Perhatikan gambar berikut!
Rumus Luas dan Keliling Trapesium Lengkap dengan Contoh Soal
Keliling dan luas pada trapesium diatas adalah …
Jawab:
Keliling trapesium:
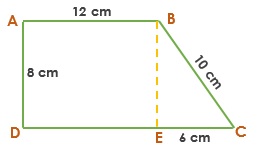
Perhatikan gambar diatas, ABED membentuk bangun persegi panjang, maka panjang AB = DE = 12 cm,
sehingga,
CD = CE + DE = 12 + 6 = 18 cm
Keliling = AB + BC + CD + DA
Keliling = 12 + 10 + 18 + 8 = 48 cm
Luas trapesium:
L = ½ × jumlah rusuk sejajar × tinggi
(BE adalah tinggi trapesium, karena ABED membentuk bangun persegi panjang, maka panjang AD = BE = 8 cm)
Sehingga,
- L = ½ × (AB + CD) × BE
- L = ½ × (12 + 18) × 8 = 120 cm
5. Sebuah benda berbentuk trapesium dengan sisi-sisi yang sejajar adalah 15 m dan 18 m serta tingginya 12 m. Luas trapesium tersebut adalah ….
Jawab:
Luas trapesium = sisi sejajar × t / 2
= ( 15 m + 18 m ) × 12 / 2
= 33 m × 6 m
= 198 m2
6. Jika sebuah trapesium yang mempunyai panjang sisi yang sejajar berturut-turut yaitu 4 cm dan 10 cm serta tinggi 5 cm. Cari dan hitunglah luas trapesium tersebut!
Diketahui :
sisi sejajar = a1 = 4 cm,
b1 = 10 cm
t = 5 cm
ditanya : L = …?
Jawab :
L = ½ x (a1 + a2) x t
L = ½ x (4 cm + 10 cm) x 5 cm
L = ½ x 14 x 5
L =Â 35 cm2
Jadi, luas trapesium tersebut adalah = 35 cm2
7. Diketahui ada sebuah luas trapesium = 104 cm2, dan panjang sisi sejajarnya adalah 15 cm dan 11 cm. Cari dan hitunglah tinggi trapesium tersebut!
Diketahui :
a = 15 cm
b = 11 cm
L =104 cm2
ditanya : t =…?
Jawab :
t =2L : (a + b)
t =2. 104 : (15 + 11)
t =208 : 26
t =8 cm2
Jadi, tinggi trapesium tersebut adalah = 8 cm2
Nah, itu tadi contoh soal trapesium sekaligus pembahasannya secara lengkap. Semoga bermanfaat untuk Anda.
Editor: Muchammad Zakaria
Download berbagai jenis aplikasi terbaru, mulai dari aplikasi windows, android, driver dan sistem operasi secara gratis hanya di Nesabamedia.com: